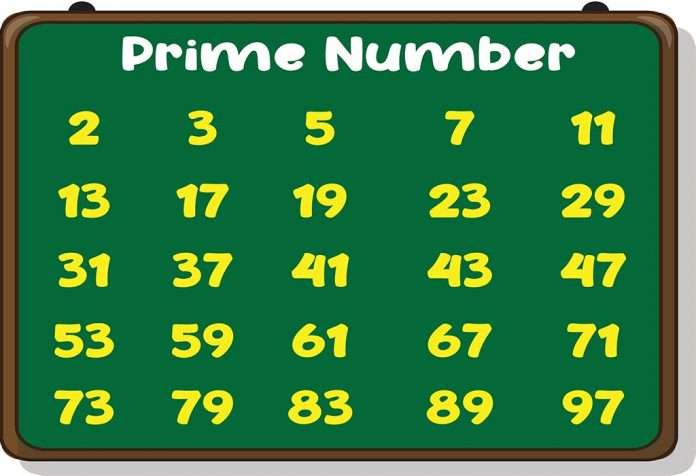
How many prime number between 1 to 100 There are 25 prime numbers between 1 and 100. Prime numbers are natural numbers greater than 1 that have no divisors other than 1 and themselves. The prime numbers in this range are: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, and 97. These numbers are essential in various fields of mathematics and have unique properties that make them fundamental to number theory. The discovery and understanding of prime numbers have been a significant focus of mathematical research for centuries.
Understanding Prime Numbers
- Definition: Prime numbers are natural numbers greater than 1 that have no positive divisors other than 1 and themselves.
- Smallest Prime: The smallest prime number is 2, which is also the only even prime number.
- Examples: Prime numbers between 1 and 100 include 2, 3, 5, 7, 11, 13, 17, and so on.
- Unique Properties: Every prime number greater than 2 is odd, as even numbers are divisible by 2.
- Fundamental Theorem of Arithmetic: Every natural number greater than 1 is either a prime itself or can be factored into prime numbers.
- Prime Factorization: The process of expressing a number as the product of its prime factors.
- Infinite Primes: There are infinitely many prime numbers, a fact proven by the ancient Greek mathematician Euclid.
- Prime Gaps: The difference between two successive prime numbers, which can vary significantly.
- Applications: Prime numbers are crucial in fields like cryptography, computer science, and number theory.
- Tests for Primality: Methods to determine if a number is prime include trial division, the Sieve of Eratosthenes, and more advanced algorithms.
- Prime Number Theorem: Describes the asymptotic distribution of prime numbers among the positive integers.
- Twin Primes: Pairs of prime numbers that have a difference of 2, such as (11, 13) and (17, 19).
- Mersenne Primes: Primes of the form 2^p – 1, where p is also a prime.
- Prime in Nature: Primes appear in biological systems, such as the life cycles of certain cicadas.
- Prime Records: The largest known prime number is continually being updated with advancements in computational methods.
Characteristics of Prime Numbers
- Divisibility: Prime numbers have exactly two distinct positive divisors: 1 and themselves.
- Smallest Prime: The smallest prime number is 2, which is also unique as the only even prime number.
- Odd Primes: All prime numbers greater than 2 are odd, as any even number greater than 2 can be divided by 2.
- Infinite Nature: There are infinitely many prime numbers, a fact established by Euclid over two millennia ago.
- Distribution: Prime numbers become less frequent as numbers get larger, but they never completely disappear.
- Prime Factorization: Every integer greater than 1 can be uniquely represented as a product of prime numbers, according to the Fundamental Theorem of Arithmetic.
- No Patterns: Prime numbers do not follow a regular pattern or sequence, making their distribution seemingly random.
- Prime Gaps: The gaps between consecutive prime numbers vary and can be large, but there is always another prime eventually.
- Twin Primes: Some primes come in pairs called twin primes, which differ by exactly 2 (e.g., 11 and 13, 17 and 19).
- Special Forms: Some primes have special forms, such as Mersenne primes (2^p – 1) and Fermat primes (2^(2^n) + 1).
- Applications in Cryptography: Prime numbers are fundamental in modern cryptographic algorithms, ensuring secure communication.
- Primality Testing: Several methods, such as the Sieve of Eratosthenes and advanced computational algorithms, are used to test the primality of numbers.
- Prime Number Theorem: This theorem describes the asymptotic distribution of prime numbers among the positive integers, providing an approximation of their density.
- Biological Occurrence: Primes appear in nature, such as the periodic life cycles of cicadas that use prime numbers to avoid predators.
- Unpredictability: Despite extensive research, predicting the occurrence of the next prime number remains a challenge.
Finding Prime Numbers
- Definition: A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself.
- Trial Division Method:
- Check divisibility by all integers up to the square root of the number.
- If the number is not divisible by any of these, it is a prime.
- Sieve of Eratosthenes:
- List all numbers up to a desired limit.
- Repeatedly mark the multiples of each prime starting from 2.
- The remaining unmarked numbers are primes.
- Primality Test Algorithms:
- More advanced methods like the Miller-Rabin primality test are used for larger numbers.
- These algorithms offer probabilistic checks for primality.
- Divisibility Rules:
- Helps quickly rule out non-prime numbers.
- For example, any even number greater than 2 is not prime.
- Prime Factorization:
- Breaking down a number into its prime components.
- If a number can be factored into primes, those factors are prime numbers.
- Mathematical Properties:
- Properties such as Fermat’s Little Theorem are used in more complex primality testing.
- Computer Algorithms:
- Efficient algorithms implemented in software to find and verify large prime numbers.
- Used extensively in cryptography and data security.
- Prime Gaps:
- The difference between consecutive prime numbers.
- Helps in identifying patterns and distributions of primes.
- Checking Small Numbers:
- For smaller ranges, manual checking and simple algorithms suffice.
- Often used for educational purposes and introductory number theory.
Conclusion
FAQs
Q: 1 How many prime numbers are there between 1 and 100?
Ans:: There are 25 prime numbers between 1 and 100.
Q: 2 What is the smallest prime number between 1 and 100?
Ans: The smallest prime number between 1 and 100 is 2.
Q:3What is the largest prime number between 1 and 100?
Ans: The largest prime number between 1 and 100 is 97.
Q: 4Are all odd numbers between 1 and 100 prime?
Ans: No, not all odd numbers between 1 and 100 are prime. Only specific odd numbers that have no divisors other than 1 and themselves are prime.






